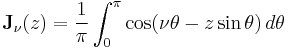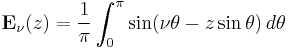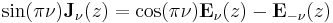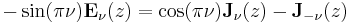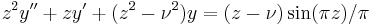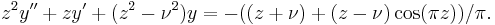Anger function
In mathematics, the Anger function, introduced by C. T. Anger (1855), is a function defined as
and is closely related to Bessel functions.
The Weber function, introduced by H. F. Weber (1879), is a closely related function defined by
and is closely related to Bessel functions of the second kind.
Relation between Weber and Anger functions
The Anger and Weber functions are related by
so in particular if ν is not an integer they can be expressed as linear combinations of each other. If ν is an integer then Anger functions Jν are the same as Bessel functions Jν, and Weber functions can be expressed as finite linear combinations of Struve functions.
Differential equations
The Anger and Weber functions are solutions of inhomogenous forms of Bessel's equation 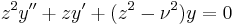 . More precisely, the Anger functions satisfy the equation
. More precisely, the Anger functions satisfy the equation
and the Weber functions satisfy the equation
References
- Abramowitz, Milton; Stegun, Irene A., eds. (1965), "Chapter 12", Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables, New York: Dover, pp. 498, ISBN 978-0486612720, MR0167642, http://www.math.sfu.ca/~cbm/aands/page_498.htm.
- C.T. Anger, Neueste Schr. d. Naturf. d. Ges. i. Danzig, 5 (1855) pp. 1–29
- Paris, R. B. (2010), "Anger-Weber Functions", in Olver, Frank W. J.; Lozier, Daniel M.; Boisvert, Ronald F. et al., NIST Handbook of Mathematical Functions, Cambridge University Press, ISBN 978-0521192255, MR2723248, http://dlmf.nist.gov/11.10
- Prudnikov, A.P. (2001), "Anger function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=A/a012490
- Prudnikov, A.P. (2001), "Weber function", in Hazewinkel, Michiel, Encyclopedia of Mathematics, Springer, ISBN 978-1556080104, http://www.encyclopediaofmath.org/index.php?title=W/w097320
- G.N. Watson, "A treatise on the theory of Bessel functions", 1–2, Cambridge Univ. Press (1952)
- H.F. Weber, Zurich Vierteljahresschrift, 24 (1879) pp. 33–76